Hydrology vs. "climate science"
A contrast based on my new paper "When are models useful? Revisiting the quantification of reality checks"
[There is also a Greek version of the post—Υπάρχει και ελληνική έκδοση της ανάρτησης]
‘For those unfamiliar with hydrology, here is its definition by UNESCO:1
Hydrology is the science which deals with the waters of the earth, their occurrence, circulation and distribution on the planet, their physical and chemical properties and their interactions with the physical and biological environment, including their responses to human activity.
As per climate, there is also a science that deals with it and its name is climatology. So, what is "climate science", a more recent name that has come to the fore in the last few decades? My interpretation is that it is a euphemism for “climate sophistry”. And we should always have in mind the following quotation by John R. Searle:2
A good rule of thumb to keep in mind is that anything that calls itself 'science' probably isn't.
Hydrology has close links with civil engineering as it is very important for the design and management of infrastructures.3 This has been fortunate, as it kept its feet on the ground of the real world and prevented it from taking off into virtual realities.
Hydrosystems, the systems that hydrology deals with, are complex and so its models rely on observational data. Analyses of data need to be based on stochastics. Understandably, hydrology has been an importer of ideas from the scientific discipline of stochastics and other related fields. There are a few exceptions where it has been an exporter. One of these is the Hurst-Kolmogorov behaviour, which was presented in an earlier post: The Nile’s gifts for understanding climate – Part 3. The other is a simple statistic to assess if a model is useful, called the Nash–Sutcliffe efficiency (NSE).
The first was pioneered by the British hydrologist H.E. Hurst4, who devoted his entire career to the measurement and study of the Nile. The other was proposed by the Irish civil engineer and hydrologist J.E. Nash and the Anglo-Irish hydrologist J.V. Sutcliffe5, in a study that for a long time has been the most cited hydrological paper (currently about 28 000 citations in Google Scholar and more than 18 000 in Scopus). Its use has been common beyond hydrology, such as in geophysics, earth sciences, atmospheric sciences, environmental sciences, statistics, engineering, data science, and computational intelligence.
My latest paper that appeared the other day is the following and is related to that by Nash and Sutcliffe:
D. Koutsoyiannis, When are models useful? Revisiting the quantification of reality checks, Water, 17 (2), 264, doi:10.3390/w17020264, 2025.
I am copying below the Discussion and Conclusions section, which provides a summary of the study:
The classical Nash–Sutcliffe efficiency appears to be a good metric of the appropriateness of a model. Yet its fusion of two different characteristics, the explained variance and the bias, is not always useful. The bias could be a very important characteristic to consider for a physically based model, where the bias reflects a violation of a physical law (e.g., conservation of mass or energy). In such cases, a large bias would be a sufficient reason to reject a model, even if it captures the variation patterns.
In other cases, in which the model is of a conceptual or statistical, rather than physical, type, the bias can be easily removed by a shift in the origin. In such cases, a nonlinear transformation of the observed and modeled series, accompanied by a linear transformation of the simulated series […], can potentially improve the agreement between the model and reality. It is suggested that in such cases, the quantified assessment of model usefulness be based on the metrics of both the original and the transformed series.
The typical metrics that are currently used to assess model performance are based on classical statistics up to a second order. This is not a problem when the processes are Gaussian, but most hydrological processes are non-Gaussian. The concept of knowable moments (K-moments) offers us a basis for extending the performance metrics to high orders, up to the sample size. The two metrics proposed, the K-unexplained variation, KUV_p, and the K-bias, KB_p, both based on K-moments of the model error, provide ideal means to assess the agreement of models with reality; the closer to zero they are, the better the agreement. The lowest order on which they are evaluated is p = 2, which represents second-order properties, but also using higher orders gives useful information on the agreement of the entire distribution functions.
The real-world application presented is a large-scale comparison of climatic model outputs for precipitation with reality over the last 84 years. It turns out that the precipitation simulated by the climate models does not agree with reality on the annual scale, but there is some improvement on larger time scales on a hemispheric basis. However, when the areal scale is decreased from hemispheric to continental, i.e., when Europe is examined, the model performance is poor even at large time scales. Therefore, the usefulness of climate model results for hydrological purposes is doubtful.
From a practical point of view, in order for a model to be useful, the NSE metric, which compares model simulations to reality, must be close to one. If it is zero, it means that using the model is no better than replacing it with just a single number, the average of observations. If it is negative, it means you’d better throw the model away.
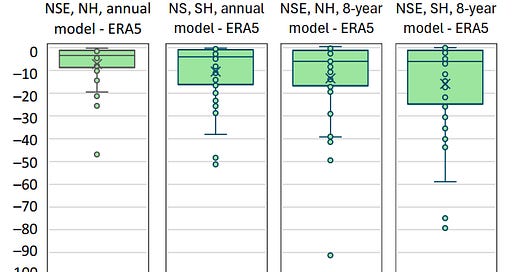
Here is a depiction the performance of 37 climate models (all models whose results are publicly available through the KNMI Climexp platform). To make time series that represent reality, the gridded data of the ERA5 reanalysis were used in the paper as the basis for assessing the models’ performance. In most cases the NSE is not just negative—it’s highly negative, even on spatial scales as big as the hemispheric.

The two climate models with the “least poor” performance were further investigated in the paper for Europe. Here are their comparisons with the ERA5 time series, which represents reality.

And here are the performance indices based on the framework proposed in the paper, the K-explained variation, which is more favourable for a model than the NSE, because it excludes the bias. Again negative results.

The question then arises: Do hydrologists use these useless climate model results? The answer is affirmative. While they would never use a hydrological model with a negative performance index, they eagerly use the climate model results in hydrological studies. And there are myriads of hydrological papers using them.
Why is this? A typical answer is that climate models are the best available technology. This is a doubly invalid argument. First, if the best available technology enables us to construct a two-storey building, we wouldn’t use it to build a skyscraper, would we? Second, it’s not true that climate models are the best available technology. Stochastic models are much simpler, less algorithmic-intensive, needing less powerful supercomputers (which, despite being also money-intensive, are ultimately misleading), but more thought- and knowledge-intensive. An example where stochastic models have performed much better than climate models on a real-world problem is the management of a long-lasting and intensive drought in Athens.6
PS. The real reason for using climate model results in hydrological studies is that climate models are the best available technology for earning money from research funds.
J. R. Searle, Minds, Brains and Science, Harvard University Press: Cambridge, MA, USA, 1984.
H.E. Hurst, Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. , 116, 770–799, 1951.
J.E. Nash and J. V. Sutcliffe, River flow forecasting through conceptual models, part I—A discussion of principles. J. Hydrol., 10, 282–290, 1970.
D. Koutsoyiannis, A. Efstratiadis, and K. Georgakakos, Uncertainty assessment of future hydroclimatic predictions: A comparison of probabilistic and scenario-based approaches, Journal of Hydrometeorology, 8 (3), 261–281, doi:10.1175/JHM576.1, 2007.
D. Koutsoyiannis, Hurst-Kolmogorov dynamics and uncertainty, Journal of the American Water Resources Association, 47 (3), 481–495, doi:10.1111/j.1752-1688.2011.00543.x, 2011.